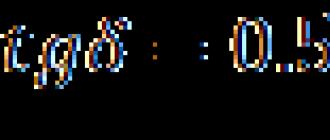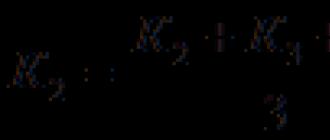This theorem is constructive, since it allows us to construct for each function a formula realizing it in the form of a perfect d.s. f. To do this, in the truth table for each function, we mark all the lines in which
Share work on social networks
If this work does not suit you, there is a list of similar works at the bottom of the page. You can also use the search button
Aranov Viktor Pavlovich Discrete Math.
Section 4. Functional systems with operations. Algebra of logic.
Lecture 21. The principle of duality. Decomposition of functions in variables. Perfect DNF and CNF
Lecture 21 PRINCIPLE OF DUALITY. BOOLEAN DECOMPOSITION
FUNCTIONS ON VARIABLES. PERFECT DISJUNCTIVE AND
CONJUNCTIVE NORMAL FORMS
Lecture plan:
- The principle of duality.
- Decomposition of boolean functions in variables. Perfect disjunctive and conjunctive normal forms.
- Principle of Duality
A function equal to is called dual function to function.
Obviously, the truth table for the dual function is obtained from the truth table for the function by inverting (ie, replacing 0 with 1 and 1 with 0) the values of the variables and the function. For instance, .
It is easy to establish for functions 0, 1 that
- function 0 is dual to 1;
- function 1 is dual to 0;
- the function is dual;
- the function is dual;
- the function is dual;
- the function is dual.
It follows from the definition of duality that
i.e., the function is dual to (property of reciprocity).
The principle of duality.If a formula implements a function, then the formula, that is, the formula obtained from the replacement of functions by, respectively, implements the function.
The formula will be called the formula dual to k.
To prove this assertion, it is necessary to verify its validity for the elementary steps of the superposition and.
Let, for example, a function be obtained from a function as a result of the following variable substitution:
Then
i.e., the function is obtained from as a result of the same variable substitution.
Let us prove the validity of the duality principle for a step using an example. Let
Then
i.e., a function is obtained from and in the same way as a function from and.
The principle of duality makes it possible to simplify the derivation of basic tautologies and has a number of useful applications, which will be discussed later.
Example 1 Identity follows from identity.
Really,
;; .
Example 2 Construction of a formula for the negation of a function.
From the definition of the dual function it follows
We get the following rule: let the formula implements the function. To get a formula for a function, you need to replace all variables in the formula with their negations.
Find the negation for the function.
Since then.
- Decomposition of boolean functions in variables. Perfect
Disjunctive and conjunctive normal forms
We introduce the notation
where is a parameter equal to either 0 or 1. Obviously,
It is easy to see that 1 if and only if.
Theorem on the expansion of functions in variables. Each function of the algebra of logic for any () can be represented in the following form:
, (1)
where the disjunction is taken over all possible sets of variable values.
This presentation is calledexpansion of a function in variables.
Proof. Consider an arbitrary set of variable values and show that the left and right parts of relation (1) take the same value on it. The left side gives. Right -
As corollaries of the theorem, we consider two special cases of decomposition.
- Variable expansion:
The functions and are calleddecomposition components.This decomposition is useful when some properties are established by induction.
- Expansion in all variables:
When identically not equal to 0, it can be transformed:
As a result, we finally get
. (2)
Such a decomposition is calledperfect disjunctive normal form(Perfect Doctor of Science).
Directly to the concept of a perfect d.s. f. adjoins the following theorem.
Theorem. Each function of the algebra of logic can be represented by a formula in the basis.
Proof. 1) Let. Then obviously
- Let it not be identically equal to 0. Then it can be represented by formula (2).
This theorem is constructive, since it allows us to construct for each function a formula realizing it in the form of a perfect d.s. f. To do this, in the truth table for each function, we mark all the lines in which. For each such row, we form a logical product, and then we connect all the resulting conjunctions with a disjunction sign.
Example 3 Find the perfect d.s. f. for the function.
Perfect d.s. f. is an expression of type P. Let us show that, when 1 is not identically equal to 1, it can be represented in the form Let us write down for the dual function (obviously not identically equal to 0) the expansion in the form of a perfect d.s. f.:
From the principle of duality it follows
Thus, we get a decomposition calledperfect conjunctive normal form(perfect Ph.D.):
. (3)
Example 4 Build a perfect Ph.D. f. for the function.
We have.
Other related works that may interest you.vshm> |
|||
| 200. | Normal Forms of Boolean Functions | 63.53KB | |
| Normal Forms of Boolean Functions The representation of a Boolean function in the form of a disjunction of conjunctive terms of unit constituents Ki 2.7 is called the disjunctive normal form of the DNF of this function. contain exactly one by one all logical variables taken with or without negations, then this form of representation of the function is called the perfect disjunctive normal form of the SDNF of this function. As you can see, when compiling an SDNF function, you need to make a disjunction of all minterms for which the function takes the value 1. | |||
| 9015. | METHODS FOR MINIMIZING BOOLEAN FUNCTIONS | 81.74KB | |
| DNF and schemes from FE. Minimization of Boolean functions based on the construction of dead-end DNFs. Minimization of Boolean functions based on the construction of dead-end DNFs Reduced dead-end and minimal DNFs are in the following relation. A dead-end DNF is obtained from a reduced DNF by removing some members. | |||
| 9017. | THE PROBLEM OF MINIMIZING BOOLEAN FUNCTIONS. GEOMETRIC INTERPRETATION | 109.86KB | |
| DNF and schemes from FE. GEOMETRIC INTERPRETATION Lecture plan: Concept of disjunctive normal form of DNF. The concept of DNF. The expression for where is the elementary conjunction of rank is called the disjunctive normal form of DNF. | |||
| 14731. | Expansion of signals into a generalized Fourier series in terms of systems of orthogonal functions. Walsh functions | 38.95KB | |
| Expansion of signals into a generalized Fourier series in terms of systems of orthogonal functions. Familiarize yourself with the basic characteristics of signals and interference. To study the representation of signals in the form of a generalized Fourier series in terms of systems of orthogonal functions. Expansion of signals into a generalized Fourier series in terms of systems of orthogonal functions. | |||
| 6707. | Designing relational databases. Design problems in the classical approach. Normalization principles, normal forms | 70.48KB | |
| What is a relational database design? It is a set of interrelated relationships in which all attributes are defined, the primary keys of the relationship are set, and some additional relationship properties are set that relate to the principles of maintaining integrity. Therefore, the design of the database must be very precise and verified. In fact, the database project is the foundation of the future software package that will be used for a long time and by many users. | |||
| 4849. | Forms and methods of implementation of the functions of the state | 197.3KB | |
| The term "function" has a different meaning in domestic and foreign scientific literature. In philosophical and general sociological terms, it is considered as "an external manifestation of the properties of an object in a given system of relations"; as a set of ordinary or specific actions of individuals or bodies | |||
| 1790. | Expansion into terms | 180.15KB | |
| The very word algorithm resembles algorithmi - the Latin form written in the name of the great mathematician of the IX century. al-Khwarizmi, who formulated the rules for vikonnanny arithmetic diy. Randomly based on algorithms and only understood the rules for vikonnanny chotirioh arithmetic diy over rich digital numbers. | |||
| 2690. | Studying the performance of drills with variable helix pitch | 18.85KB | |
| Models of the cutting process can be represented by a system of mathematical equations that determine in each case the evaluation function or criteria for the performance of cutting tools, as well as technical restrictions on the kinematics of the machine tool, the rigidity of the cutting tools and the entire technological system. | |||
| 17088. | CRIMINAL LIABILITY FOR CRIMES COMMITTED AS PART OF AN ORGANIZED CRIMINAL GROUP | 50.97KB | |
| Lomtev GENERAL DESCRIPTION OF THE WORK The relevance of the research topic is determined by the need for further development and improvement of the theory and practice of implementing criminal liability for crimes committed as part of an organized criminal group. Research in the field of combating organized crime shows that the most dangerous and hard-to-solve crimes are committed within organized criminal groups. As part of solving the problem of increasing the effectiveness of the criminal law in terms of combating... | |||
| 11576. | The concept, types and forms of transactions. Consequences of non-compliance with the required form of transactions | 49.82KB | |
| Recognition of the transaction as invalid types of invalid transaction. The applied value of the course work is to simplify the concept of a transaction, that is, its public presentation in a more accessible form. | |||
Setting Boolean functions of variables using the truth table, defining a formula, types of the most important equivalences (laws) of the algebra of logic. Equivalent formulas, laws of equivalence, logical equations. Decomposition of boolean functions in variables.
By clicking on the "Download archive" button, you will download the file you need for free.
Before downloading this file, remember those good essays, control, term papers, theses, articles and other documents that are unclaimed on your computer. This is your work, it should participate in the development of society and benefit people. Find these works and send them to the knowledge base.
We and all students, graduate students, young scientists who use the knowledge base in their studies and work will be very grateful to you.
To download an archive with a document, enter a five-digit number in the field below and click the "Download archive" button
Similar Documents
Basic axioms and identities of the algebra of logic. Analytical form of representation of Boolean functions. Elementary functions of the algebra of logic. Functions of the algebra of logic of one argument and forms of its realization. Properties, features and types of logical operations.
abstract, added 12/06/2010
The concept of the algebra of logic, its essence and features, basic concepts and definitions, the subject and methodology of study. Laws of the algebra of logic and consequences from them, methods for constructing formulas according to a given truth table. Forms of representation of Boolean functions.
tutorial, added 04/29/2009
Boolean algebras are lattices of a special type used in the study of logic (both the logic of human thinking and digital computer logic), as well as switching circuits. Minimal forms of Boolean polynomials. Theorems of abstract boolean algebra.
term paper, added 05/12/2009
Operations on logical statements: Boolean functions and the expression of some of these dependencies through others. Propositional formulas and some laws of propositional logic. Translation of natural language expressions into symbolic speech of the algebra of logic.
test, added 04/26/2011
Logic is the science of the laws and forms of thinking, and the basic concept of the algebra of logic is a statement. Basic concepts and identities of Boolean algebra. The study of methods for minimizing Boolean functions. Quine's method based on the application of two basic relationships.
test, added 01/20/2011
Basic concepts of the algebra of logic. Disjunctive and conjunctive normal forms. Essence of Shannon's theorem. Boolean functions of two variables. Series and parallel connection of two switches. Properties of elementary functions of the algebra of logic.
test, added 11/29/2010
Boolean variable in the algebra of logic. Logical operations: negation, conjunction, disjunction, implication, equivalence. Basic laws of the algebra of logic. Rules for minimizing a logical function (getting rid of the operations of implication and equivalence).
term paper, added 01/16/2012
We select the variable x 1 and consider the function f with respect to it.
The whole set of sets the truth table is divided into two subsets, each of which has four sets<0, a 2 , a 3 >and<1, a 2 , a 3 >.
Then the function f(x 1, x 2, x 3) can be represented as a disjunction of two functions of two variables, and this formula will look like:
Consider the following formulas:
The left side of the first formula is equivalent to the right one, since for x 1 =0 and in accordance with the conjunction operation. The validity of the second formula can be shown similarly. Thus, putting these formulas in the previous disjunction, we get:
This expression is called the expansion of the function f(x 1 ,x 2 ,x 3) with respect to the variable x 1 .
Now, similarly, we can expand the functions f(0,x 2 ,x 3) and f(1,x 2 ,x 3) in x 2 . Get
Substituting these formulas into the previous ones, we get
In accordance with the distributivity of the operation &, we introduce the variable x 1 and its inversion into brackets, we get
In general, for a function f(x 1 ,x 2 ,..,x n) of n variables, the expansion in m variables (m £ n) has the form
where the disjunction is taken over all 2 m sets of variables x 1 ,x 2 ,..,x m .
Consider the decomposition (*4) in the extreme case when m=n. (see example (*3)).
Then in all conjunctions the values of the function f on each fixed set have values equal to zero or one. Removing all zero conjunctions, we obtain a new decomposition, and in this new decomposition we remove the factors of functions in the conjunctions, because they are equal to 1. The remaining expression is called CDNF (perfect disjunctive normal form).
Let's do all this for example (*3).
After removing from (*3) conjunctions with zero values of the function f on the given sets, we get:
Since according to the truth table
f(0,0,0) = f(0,1,0) = f(1,1,0) = f(1,1,1)=1
then from the conjunctions we remove the factors of the functions, after which we get:
This is the perfect disjunctive normal form of the Boolean function f.
Lemma. Any Boolean function (except for the constant "0") has a PDNF, and only one.
Similarly, you can enter the conjunctive form,
Construction of SDNF for a function given by a table
This corollary is constructive, since according to the function table, it allows you to construct a formula that is SDNF (if ).
sdnf functions f contains exactly as many conjunctions as there are ones in the table f; to each “single” set (d 1 ,…,d n), those. the set on which the value of the function is equal to 1 corresponds to the conjunction of all variables in which x i taken with a negative if d i=0, and without negation if d i =1.
Consider the question of representation n-local boolean function f(x 1 ,x 2 ,…,x n) by some propositional algebra formula.
Let's introduce the notation, where is a parameter equal to 0 or 1.
It's obvious that ![]()
Theorem 1.1. Every function of the algebra of logicf(x 1 , x 2 ,…, x n ) for anym(1£ m £ n) can be represented in the following form:
where the disjunction is taken over all possible sets of values of the variables .
Proof. Consider an arbitrary set of values of all variables of a given function. Let us show that on this set the left and right parts of formula (1) take the same value. The left side is ![]() , right
, right
because , if only , if , then the corresponding logical term can be discarded.
Comment. The representation of the function specified in the theorem is called the expansion of the function in terms of m variables .
Corollary 1(expansion in one variable).
In this case, the functions ![]() and
and ![]() called decomposition components.
called decomposition components.
Consequence 2(expansion in all variables).
It is obvious that if ![]() , then
, then
So if the function f(x 1 ,x 2 ,…,x n) is not an identically false function, then it can be expressed by an equivalent formula, which is a logical sum of different products of the form , and such a representation is unique.
The form of formula (2) can be greatly simplified. It is known that any formula of the algebra of logic can be reduced by means of equivalent transformations to a formula containing only conjunction and negation or disjunction and negation. As a result of carrying out equivalent transformations, several formulas can be obtained, however, only one of them will have the following properties:
1. Each logical term contains all the variables included in the formula f(x 1 ,x 2 ,…,x n).
2. No logical term contains both a variable and its negation.
3. All logical terms in the formula are different.
4. No logical term contains the same variable twice.
These four properties are called properties of perfection(or properties of C).
If f(x 1 ,x 2 ,…,x n) is given by the truth table, then the corresponding logic algebra formula can be restored quite simply. For all argument values x 1 ,x 2 ,…,x n, at which f takes the value 1, you need to write down the conjunction of the elementary variables of the propositions, taking for the term of the conjunction x i, if x i=1, and if x i=0. The disjunction of all recorded conjunctions will be the necessary formula. About values f 0 you don't have to worry, because the corresponding term in the formula will be equal to 0 and can be discarded due to the equivalence fÚ 0 ≡ f.
For example, let the function f(x, y, z) has the following truth table:
|
x |
y |
z |
f(x, y, z) |
Decomposition of boolean functions in variables.
Let G be a parameter equal to 0 or 1. Let us introduce the notation:

It is easy to check by checking that x G = 1 if and only if x= G. It follows that the conjunction is equal to 1 (here G is equal to 0 or 1) if and only if ![]() . For example, the conjunction (in which G 2 \u003d G 1 \u003d 0, G 3 \u003d G 4 \u003d 1) is 1 only if x 1 = x 2 = 0, x 3 = x 4 = 1.
. For example, the conjunction (in which G 2 \u003d G 1 \u003d 0, G 3 \u003d G 4 \u003d 1) is 1 only if x 1 = x 2 = 0, x 3 = x 4 = 1.
Theorem 1Any Boolean function f(x 1 ,x 2 ,…,x n) must be represented in the following form:
where 1 ≤ k ≤ n, in the disjunction is taken over all sets of variable values.
This representation is called the expansion of the function in terms of variables. For example, for n = 4, k = 2, expansion (3.1) has the form:
![]() .
.
Let us prove the expansion (3.1). To do this, take an arbitrary set of variable values ![]() . Let us show that the left and right sides of relation (3.1) take on the same value. Indeed, since x G = 1 if and only if x= G, then among 2 only one conjunction of the right-hand side of (3.1) turns to unity, in which
. Let us show that the left and right sides of relation (3.1) take on the same value. Indeed, since x G = 1 if and only if x= G, then among 2 only one conjunction of the right-hand side of (3.1) turns to unity, in which ![]() . All other conjunctions are equal to zero.
. All other conjunctions are equal to zero.
For this reason . As a corollary of expansion (3.1), we obtain the following two special expansions.
Variable expansion x n:
If the Boolean function is not a constant 0, then the expansion is valid
Expansion in all variables:
, ![]() (3.3)
(3.3)
where the disjunction is taken over all sets ![]() , for which the value of the function
, for which the value of the function ![]() equals 1.
equals 1.
Decomposition (3.3) is usually called the perfect disjunctive normal form (abbreviated notation SDNF) of the function.
Decomposition (3.3) gives a way to construct an SDNF. To do this, in the truth table, mark all the rows ![]() , in which
, in which ![]() . For each such row, we form a conjunction and then connect all the resulting conjunctions with a disjunction sign.
. For each such row, we form a conjunction and then connect all the resulting conjunctions with a disjunction sign.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, there is a one-to-one correspondence between the truth table of a function ![]() and her SDNF. And this means that the SDNF for the Boolean function is unique.
and her SDNF. And this means that the SDNF for the Boolean function is unique.
A single boolean function that does not have a sdnf is the constant 0.
Example 1 Find the perfect disjunctive form for a function ![]() .
.
Let's make a truth table for this function:
| |
|||||
From here we get: ![]() = = .
= = .
An important role in the algebra of logic is played by the following decomposition of Boolean functions.
Theorem 2Any boolean function ![]() must be presented in the following form:
must be presented in the following form:
where 1≤k≤n, and the conjunction is taken over all 2 k sets of variable values.
Indeed, let ![]() is an arbitrary set of variable values. Let us show that the left and right parts of relation (3.4) take on the same value. Since only when , then among 2 k disjunctions
is an arbitrary set of variable values. Let us show that the left and right parts of relation (3.4) take on the same value. Since only when , then among 2 k disjunctions ![]() on the right-hand side of (3.4) only one vanishes, in which
on the right-hand side of (3.4) only one vanishes, in which ![]() . All other disjunctions are equal to 1.
. All other disjunctions are equal to 1.
For this reason ![]() = =
= = ![]() .
.
Expansions of Boolean functions follow directly from expansion (3.4):
The last decomposition is called the perfect conjunctive normal form (CKNF). Decomposition (3.6) gives a way to construct the SKNF. To do this, in the truth table, we mark all the lines in which. For each such row, we form a disjunction ![]() and then we connect all the resulting conjunctions with a conjunction sign. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, there is a one-to-one correspondence between the truth table of a function
and then we connect all the resulting conjunctions with a conjunction sign. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, there is a one-to-one correspondence between the truth table of a function ![]() and her SKNF. And this means that the SKNF for the Boolean function is unique.
and her SKNF. And this means that the SKNF for the Boolean function is unique.
The only boolean function that does not have SKNF is the constant 1.
Example 2 Find the perfect conjunctive normal form for a function ![]() .
.
Let's make a truth table for this function.
| |
|||||
From here we get SKNF
Form formula (short notation), where ![]() - conjunctions
- conjunctions ![]() called disjunctive normal form (DNF).
called disjunctive normal form (DNF).
By virtue of the above definition of DNF, there will be, for example, expressions: , .
As noted in paragraph 2.2, all logical operations can be reduced to three: conjunctions, disjunctions and denials. Moreover, in view of de Morgan's law, the negation sign can be assumed to apply only to variables.
Now, using the distributive law, we open the brackets and get the disjunctive normal form. So, the following theorem is true.
Theorem 3 For any formula of the algebra of logic, there exists a disjunctive normal form equivalent to it.
The proof of this theorem gives a way to construct a disjunctive normal form for any formula in the algebra of logic.
Example 3 Find the disjunctive normal form for the following formula: ![]() .
.
Excluding sign by law ![]() and applying the laws of de Morgan and double negation, we get:
and applying the laws of de Morgan and double negation, we get:
![]()
Then, applying the law of distributivity, we expand the brackets
The last expression is the disjunctive normal form.
View form ![]() (short notation), where are disjunctions
(short notation), where are disjunctions ![]() called conjunctive normal form (CNF).
called conjunctive normal form (CNF).
These are, for example, expressions:
![]() , .
, .
As shown above, for any formula of the algebra of logic there exists a disjunctive form equivalent to it. Using the distributive law , it is easy to obtain a CNF from a given DNF.
So, the following theorem is true.
Theorem 4 For any formula of the algebra of logic, there exists a conjunctive normal form equivalent to it.
The proof of this theorem gives a way to construct a conjunctive normal form for any formula in the algebra of logic.
Example 4 Find disjunctive and conjunctive normal forms for the following formula: .
Using the law ![]() , we exclude the sign . We get the formula.
, we exclude the sign . We get the formula.
Using de Morgan's law, we obtain the formula ![]() . Expanding the brackets, we obtain the disjunctive normal form
. Expanding the brackets, we obtain the disjunctive normal form
![]() .
.
To get the conjunctive normal form, apply to the formula ![]() distributive law, we get:
distributive law, we get:
The last expression is the conjunctive normal form. Since and , the resulting CNF is equivalent to the following CNF:
Among all the normal formulas of this formula, we single out the perfect normal form, both disjunctive and conjunctive. Considering expansion (3), it is easy to see that the perfect disjunctive normal form of a formula of the algebra of logic containing exactly n distinct variables is its disjunctive normal form, in which:
1) all conjunctions are pairwise distinct;
2) each conjunction contains exactly n variables;
3) in each conjunction there are all n variables.
In Example 1, we have considered one of the ways to construct an SDNF based on the compilation of a truth table. The next way to construct SDNF is based on the application of the laws of the algebra of logic.
Example 5 Find the perfect disjunctive form of the formula .
Using that ![]() , we get . In view of de Morgan's laws and double negation, we have obtained a disjunctive normal form. This DNF is equivalent to the formula .
, we get . In view of de Morgan's laws and double negation, we have obtained a disjunctive normal form. This DNF is equivalent to the formula .
Expanding the brackets, we get: .
Using the law of idempotency, we obtain the required SDNF:
Taking into account the decomposition (3.6), it is easy to see that the perfect conjunctive normal form of the formula of the algebra of logic containing exactly n different variables, there is its conjunctive normal form, in which:
1) all disjunctions are pairwise distinct;
2) each disjunction contains exactly n members; identically true, if it takes on the value true.
Examples of identically true formulas are the formulas:
identically false, if it, with all the values of the variables included in it, takes on the value Lying.
Examples of identically false formulas are the formulas:
The formula of the algebra of logic is usually called doable, if for some values of the variables included in it, it takes the value true.
Examples of feasible formulas are the following formulas:
In the algebra of logic, one can pose the following problem: to indicate a method (algorithm) that allows for each formula of the algebra of logic to find out whether it is identically true or not. The task is called resolution problems.
Consider the following two ways to solve this problem.
Method 1 (table) In order to determine whether a given formula is identically true or not, it is sufficient to compile its truth table.
At the same time, this method, although it provides a fundamental solution to the solvability problem, is rather cumbersome.
Method 2 based on the reduction of formulas to normal form.
Theorem 4A formula of the algebra of logic is identically true if and only if every disjunction in its conjunctive normal form contains some variable together with its negation.
Indeed, if each disjunction in conjunctive normal form contains a variable together with its negation, then all disjunctions are equal to 1, because , . It follows that CNF is identically true.
Let now the given formula be identically true, and let ![]() there is some disjunction in the CNF of this formula. Let us assume that the given disjunction does not contain a variable together with its negation. In this case, we can give the value 0 to each variable that is not under the negation sign, and the value 1 to each variable that is under the negation sign. After this substitution, all disjunctions will become equal to 0, therefore, the formula is not identically true. We got a contradiction.
there is some disjunction in the CNF of this formula. Let us assume that the given disjunction does not contain a variable together with its negation. In this case, we can give the value 0 to each variable that is not under the negation sign, and the value 1 to each variable that is under the negation sign. After this substitution, all disjunctions will become equal to 0, therefore, the formula is not identically true. We got a contradiction.
Example 7 Find out if the formula is identically true
![]() .
.
Using that ![]() , we get .
, we get .
Applying the distributivity law, we obtain CNF:
Since every disjunction contains some variable along with its negation, the formula is identically true.
Similarly to the previous theorem, the following theorem is proved:
Theorem 5A formula of the algebra of logic is identically false if and only if every conjunction in its disjunctive form contains some variable together with its negation.
Decomposition of boolean functions in variables. - concept and types. Classification and features of the category "Decomposition of Boolean functions in variables." 2017, 2018.