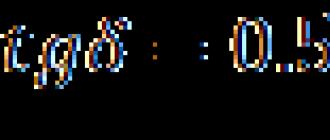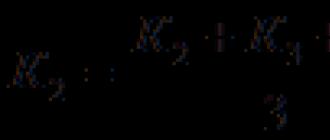Ce théorème est constructif, puisqu'il permet de construire pour chaque fonction une formule la réalisant sous la forme d'un d.s. parfait. F. Pour ce faire, dans la table de vérité de chaque fonction, on marque toutes les lignes dans lesquelles
Partager le travail sur les réseaux sociaux
Si cette oeuvre ne vous convient pas, il y a une liste d'oeuvres similaires en bas de page. Vous pouvez également utiliser le bouton de recherche
Aranov Viktor Pavlovitch Mathématiques discrètes.
Section 4. Systèmes fonctionnels avec opérations. Algèbre de la logique.
Conférence 21. Le principe de dualité. Décomposition des fonctions en variables. DNF et CNF parfaits
Conférence 21 PRINCIPE DE DUALITÉ. DÉCOMPOSITION BOOLÉENNE
FONCTIONS SUR LES VARIABLES. PARFAIT DISJONCTIF ET
FORMES NORMALES CONJONCTIVES
Plan de cours :
- Le principe de dualité.
- Décomposition de fonctions booléennes en variables. Formes normales disjonctives et conjonctives parfaites.
- Principe de dualité
Une fonction égale à s'appelle double fonction pour fonctionner.
Évidemment, la table de vérité de la fonction duale est obtenue à partir de la table de vérité de la fonction en inversant (c'est-à-dire en remplaçant 0 par 1 et 1 par 0) les valeurs des variables et de la fonction. Par exemple, .
Il est facile d'établir pour les fonctions 0, 1 que
- la fonction 0 est double de 1 ;
- la fonction 1 est double de 0 ;
- la fonction est duale ;
- la fonction est duale ;
- la fonction est duale ;
- la fonction est double.
Il découle de la définition de la dualité que
c'est-à-dire que la fonction est double de (propriété de réciprocité).
Le principe de dualité.Si une formule implémente une fonction, alors la formule, c'est-à-dire la formule obtenue à partir du remplacement des fonctions par, respectivement, implémente la fonction.
La formule sera appelée la formule duale à k.
Pour prouver cette assertion, il faut vérifier sa validité pour les étapes élémentaires de la superposition et.
Supposons, par exemple, qu'une fonction soit obtenue à partir d'une fonction à la suite de la substitution de variable suivante :
Puis
c'est-à-dire que la fonction est obtenue à partir de la même substitution de variable.
Démontrons la validité du principe de dualité pour une étape à l'aide d'un exemple. Laisser
Puis
c'est-à-dire qu'une fonction est obtenue à partir de et de la même manière qu'une fonction à partir de et.
Le principe de dualité permet de simplifier la dérivation des tautologies de base et a un certain nombre d'applications utiles, qui seront discutées plus tard.
Exemple 1 L'identité découle de l'identité.
Vraiment,
;; .
Exemple 2 Construction d'une formule de négation d'une fonction.
De la définition de la fonction duale, il résulte
On obtient la règle suivante : laisser la formule implémente la fonction. Pour obtenir une formule pour une fonction, vous devez remplacer toutes les variables de la formule par leurs négations.
Trouvez la négation de la fonction.
Depuis.
- Décomposition de fonctions booléennes en variables. Parfait
Formes normales disjonctives et conjonctives
Nous introduisons la notation
où est un paramètre égal à 0 ou 1. Évidemment,
Il est facile de voir que 1 si et seulement si.
Théorème sur le développement des fonctions en variables. Chaque fonction de l'algèbre de la logique pour tout () peut être représentée sous la forme suivante :
, (1)
où la disjonction est prise sur tous les ensembles possibles de valeurs variables.
Cette présentation s'appelledéveloppement d'une fonction en variables.
Preuve. Considérons un ensemble arbitraire de valeurs variables et montrons que les parties gauche et droite de la relation (1) prennent la même valeur sur celui-ci. Le côté gauche donne. À droite -
Comme corollaires du théorème, nous considérons deux cas particuliers de décomposition.
- Expansion variable :
Les fonctions et sont appeléescomposants de décomposition.Cette décomposition est utile lorsque certaines propriétés sont établies par induction.
- Expansion dans toutes les variables :
Lorsqu'il est identiquement différent de 0, il peut être transformé :
En conséquence, nous obtenons finalement
. (2)
Une telle décomposition est appeléeforme normale disjonctive parfaite(Parfait docteur en sciences).
Directement au concept d'un d.s. parfait. F. rejoint le théorème suivant.
Théorème. Chaque fonction de l'algèbre de la logique peut être représentée par une formule dans la base.
Preuve 1) Soit. Alors évidemment
- Qu'il ne soit pas identiquement égal à 0. Il peut alors être représenté par la formule (2).
Ce théorème est constructif, puisqu'il permet de construire pour chaque fonction une formule la réalisant sous la forme d'un d.s. parfait. F. Pour ce faire, dans la table de vérité de chaque fonction, nous marquons toutes les lignes dans lesquelles. Pour chacune de ces lignes, nous formons un produit logique, puis nous connectons toutes les conjonctions résultantes avec un signe de disjonction.
Exemple 3 Trouvez le parfait d.s. F. pour la fonction.
Parfait d.s. F. est une expression de type P. Montrons que, lorsque 1 n'est pas identiquement égal à 1, il peut être représenté sous la forme Inscrivons pour la fonction duale (évidemment pas identiquement égale à 0) le développement sous la forme d'un d.s. parfait. F.:
Du principe de dualité il découle
Ainsi, on obtient une décomposition appeléeforme normale conjonctive parfaite(doctorat parfait):
. (3)
Exemple 4 Construisez un doctorat parfait. F. pour la fonction.
On a.
Autres travaux connexes susceptibles de vous intéresser.vshm> |
|||
| 200. | Formes normales des fonctions booléennes | 63.53KB | |
| Formes normales des fonctions booléennes La représentation d'une fonction booléenne sous la forme d'une disjonction de termes conjonctifs de constituants unitaires Ki 2.7 est appelée la forme normale disjonctive du DNF de cette fonction. contiennent exactement une à une toutes les variables logiques prises avec ou sans négations, alors cette forme de représentation de la fonction est appelée forme normale disjonctive parfaite de la SDNF de cette fonction. Comme vous pouvez le voir, lors de la compilation d'une fonction SDNF, vous devez faire une disjonction de tous les minterms pour lesquels la fonction prend la valeur 1. | |||
| 9015. | MÉTHODES POUR MINIMISER LES FONCTIONS BOOLÉENNES | 81.74Ko | |
| DNF et régimes de FE. Minimisation des fonctions booléennes basée sur la construction de DNF sans issue. Minimisation des fonctions booléennes basée sur la construction de DNF sans issue Les DNF sans issue et minimaux réduits sont dans la relation suivante. Un DNF sans issue est obtenu à partir d'un DNF réduit en supprimant certains membres. | |||
| 9017. | LE PROBLÈME DE LA MINIMISATION DES FONCTIONS BOOLÉENNES. INTERPRÉTATION GÉOMÉTRIQUE | 109.86Ko | |
| DNF et régimes de FE. INTERPRÉTATION GÉOMÉTRIQUE Plan du cours : Notion de forme normale disjonctive de DNF. Le concept de DNF. L'expression de où est la conjonction élémentaire de rang est appelée la forme normale disjonctive de DNF. | |||
| 14731. | Développement des signaux en une série de Fourier généralisée en termes de systèmes de fonctions orthogonales. Fonctions de Walsh | 38.95Ko | |
| Développement des signaux en une série de Fourier généralisée en termes de systèmes de fonctions orthogonales. Familiarisez-vous avec les caractéristiques de base des signaux et des interférences. Étudier la représentation des signaux sous la forme d'une série de Fourier généralisée en termes de systèmes de fonctions orthogonales. Développement des signaux en une série de Fourier généralisée en termes de systèmes de fonctions orthogonales. | |||
| 6707. | Conception de bases de données relationnelles. Problèmes de conception dans l'approche classique. Principes de normalisation, formes normales | 70.48KB | |
| Définition d'une conception de base de données relationnelle ? Il s'agit d'un ensemble de relations interdépendantes dans lesquelles tous les attributs sont définis, les clés primaires de la relation sont définies et certaines propriétés de relation supplémentaires sont définies en rapport avec les principes de maintien de l'intégrité. Par conséquent, la conception de la base de données doit être très précise et vérifiée. En fait, le projet de base de données est la base du futur progiciel qui sera utilisé longtemps et par de nombreux utilisateurs. | |||
| 4849. | Formes et modalités de mise en œuvre des fonctions de l'État | 197.3Ko | |
| Le terme "fonction" a une signification différente dans la littérature scientifique nationale et étrangère. En termes philosophiques et sociologiques généraux, il est considéré comme « une manifestation extérieure des propriétés d'un objet dans un système de relations donné » ; comme un ensemble d'actions ordinaires ou spécifiques d'individus ou d'organismes | |||
| 1790. | Développement en termes | 180.15Ko | |
| Le mot même algorithme ressemble à algorithmi - la forme latine écrite au nom du grand mathématicien du IXe siècle. al-Khwarizmi, qui a formulé les règles du bricolage arithmétique vikonnanny. Basé au hasard sur des algorithmes et seulement compris les règles de l'arithmétique vikonnanny chotirioh diy sur des nombres numériques riches. | |||
| 2690. | Etude des performances des forets à pas d'hélice variable | 18.85Ko | |
| Les modèles du processus de coupe peuvent être représentés par un système d'équations mathématiques qui déterminent dans chaque cas la fonction d'évaluation ou les critères de performance des outils de coupe, ainsi que les restrictions techniques sur la cinématique de la machine-outil, la rigidité des outils de coupe et l'ensemble du système technologique. | |||
| 17088. | RESPONSABILITÉ PÉNALE POUR LES INFRACTIONS COMMISES DANS LE CADRE D'UN GROUPE CRIMINEL ORGANISÉ | 50.97Ko | |
| Lomtev DESCRIPTION GÉNÉRALE DU TRAVAIL La pertinence du sujet de recherche est déterminée par la nécessité de développer et d'améliorer davantage la théorie et la pratique de la mise en œuvre de la responsabilité pénale pour les crimes commis dans le cadre d'un groupe criminel organisé. Les recherches dans le domaine de la lutte contre le crime organisé montrent que les crimes les plus dangereux et les plus difficiles à résoudre sont commis au sein de groupes criminels organisés. Dans le cadre de la résolution du problème de l'augmentation de l'efficacité du droit pénal en matière de lutte... | |||
| 11576. | Le concept, les types et les formes de transactions. Conséquences du non-respect de la forme requise des opérations | 49.82Ko | |
| Reconnaissance de la transaction en tant que types invalides de transaction invalide. La valeur appliquée du travail de cours est de simplifier le concept d'une transaction, c'est-à-dire sa présentation publique sous une forme plus accessible. | |||
Définition de fonctions booléennes de variables à l'aide de la table de vérité, définition d'une formule, types des équivalences (lois) les plus importantes de l'algèbre de la logique. Formules équivalentes, lois d'équivalence, équations logiques. Décomposition de fonctions booléennes en variables.
En cliquant sur le bouton "Télécharger l'archive", vous téléchargerez gratuitement le fichier dont vous avez besoin.
Avant de télécharger ce fichier, rappelez-vous ces bons essais, contrôles, dissertations, thèses, articles et autres documents qui ne sont pas réclamés sur votre ordinateur. C'est votre travail, il doit participer au développement de la société et bénéficier aux gens. Trouvez ces œuvres et envoyez-les à la base de connaissances.
Nous et tous les étudiants, étudiants diplômés, jeunes scientifiques qui utilisons la base de connaissances dans leurs études et leur travail vous en serons très reconnaissants.
Pour télécharger une archive avec un document, entrez un numéro à cinq chiffres dans le champ ci-dessous et cliquez sur le bouton "Télécharger l'archive"
Documents similaires
Axiomes et identités de base de l'algèbre de la logique. Forme analytique de représentation des fonctions booléennes. Fonctions élémentaires de l'algèbre de la logique. Fonctions de l'algèbre de la logique d'un argument et formes de sa réalisation. Propriétés, caractéristiques et types d'opérations logiques.
résumé, ajouté le 12/06/2010
Le concept de l'algèbre de la logique, son essence et ses caractéristiques, les concepts de base et les définitions, le sujet et la méthodologie d'étude. Lois de l'algèbre de la logique et leurs conséquences, méthodes de construction de formules selon une table de vérité donnée. Formes de représentation des fonctions booléennes.
tutoriel, ajouté le 29/04/2009
Les algèbres booléennes sont des treillis d'un type spécial utilisé dans l'étude de la logique (à la fois la logique de la pensée humaine et la logique informatique numérique), ainsi que les circuits de commutation. Formes minimales des polynômes booléens. Théorèmes d'algèbre booléenne abstraite.
dissertation, ajouté le 12/05/2009
Opérations sur des énoncés logiques : fonctions booléennes et expression de certaines de ces dépendances à travers d'autres. Formules propositionnelles et quelques lois de la logique propositionnelle. Traduction d'expressions du langage naturel en discours symbolique de l'algèbre de la logique.
test, ajouté le 26/04/2011
La logique est la science des lois et des formes de pensée, et le concept de base de l'algèbre de la logique est un énoncé. Concepts de base et identités de l'algèbre booléenne. L'étude des méthodes de minimisation des fonctions booléennes. Méthode de Quine basée sur l'application de deux relations fondamentales.
test, ajouté le 20/01/2011
Concepts de base de l'algèbre de la logique. Formes normales disjonctives et conjonctives. Essence du théorème de Shannon. Fonctions booléennes de deux variables. Connexion série et parallèle de deux interrupteurs. Propriétés des fonctions élémentaires de l'algèbre de la logique.
test, ajouté le 29/11/2010
Variable booléenne dans l'algèbre de la logique. Opérations logiques : négation, conjonction, disjonction, implication, équivalence. Lois fondamentales de l'algèbre de la logique. Règles de minimisation d'une fonction logique (suppression des opérations d'implication et d'équivalence).
dissertation, ajouté le 16/01/2012
Nous sélectionnons la variable x 1 et considérons la fonction f par rapport à elle.
L'ensemble des ensembles la table de vérité est divisée en deux sous-ensembles, dont chacun a quatre ensembles<0, a 2 , a 3 >et<1, a 2 , a 3 >.
Alors la fonction f(x 1, x 2, x 3) peut être représentée comme une disjonction de deux fonctions de deux variables, et cette formule ressemblera à :
Considérez les formules suivantes :
Le membre de gauche de la première formule est équivalent au membre de droite, puisque pour x 1 =0 et conformément à l'opération de conjonction. La validité de la deuxième formule peut être démontrée de manière similaire. Ainsi, en mettant ces formules dans la disjonction précédente, on obtient :
Cette expression s'appelle le développement de la fonction f(x 1 ,x 2 ,x 3) par rapport à la variable x 1 .
Maintenant, de manière similaire, nous pouvons développer les fonctions f(0,x 2 ,x 3) et f(1,x 2 ,x 3) en x 2 . Avoir
En substituant ces formules aux précédentes, on obtient
Conformément à la distributivité de l'opération &, on introduit la variable x 1 et son inversion entre parenthèses, on obtient
En général, pour une fonction f(x 1 ,x 2 ,..,x n) de n variables, le développement en m variables (m £ n) a la forme
où la disjonction est prise sur les 2 m ensembles de variables x 1 ,x 2 ,..,x m .
Considérons la décomposition (*4) dans le cas extrême où m=n. (voir exemple (*3)).
Alors dans toutes les conjonctions les valeurs de la fonction f sur chaque ensemble fixe ont des valeurs égales à zéro ou un. En supprimant toutes les conjonctions nulles, nous obtenons une nouvelle décomposition, et dans cette nouvelle décomposition nous supprimons les facteurs des fonctions dans les conjonctions, car ils sont égaux à 1. L'expression restante est appelée CDNF (forme normale disjonctive parfaite).
Faisons tout cela par exemple (*3).
Après avoir retiré de (*3) les conjonctions à valeurs nulles de la fonction f sur les ensembles donnés, on obtient :
Puisque selon la table de vérité
f(0,0,0) = f(0,1,0) = f(1,1,0) = f(1,1,1)=1
puis des conjonctions on enlève les facteurs des fonctions, après quoi on obtient :
C'est la forme normale disjonctive parfaite de la fonction booléenne f.
Lemme. Toute fonction booléenne (à l'exception de la constante "0") a un PDNF, et un seul.
De même, vous pouvez entrer la forme conjonctive,
Construction de SDNF pour une fonction donnée par une table
Ce corollaire est constructif puisque selon la table des fonctions, il permet de construire une formule qui est SDNF (si ).
fonctions sdnf F contient exactement autant de conjonctions qu'il y en a dans le tableau F; à chaque ensemble "simple" (d 1 ,…,d n), celles. l'ensemble sur lequel la valeur de la fonction est égale à 1 correspond à la conjonction de toutes les variables dans lesquelles x je pris avec un négatif si ré je=0, et sans négation si ré je =1.
Considérez la question de la représentation n-fonction booléenne locale F(X 1 ,X 2 ,…,X n) par une formule d'algèbre propositionnelle.
Introduisons la notation, où est un paramètre égal à 0 ou 1.
Il est évident que ![]()
Théorème 1.1. Chaque fonction de l'algèbre de la logiqueF(X 1 , X 2 ,…, X n ) pour toutem(1£ m £ n) peut être représenté sous la forme suivante :
où la disjonction est prise sur tous les ensembles possibles de valeurs des variables .
Preuve. Considérons un ensemble arbitraire de valeurs de toutes les variables d'une fonction donnée. Montrons que sur cet ensemble les parties gauche et droite de la formule (1) prennent la même valeur. Le côté gauche est ![]() , à droite
, à droite
car , si seulement , si , alors le terme logique correspondant peut être ignoré.
Commenter. La représentation de la fonction spécifiée dans le théorème est appelée le développement de la fonction en termes de m variables.
Corollaire 1(développement en une variable).
Dans ce cas, les fonctions ![]() et
et ![]() appelé composants de décomposition.
appelé composants de décomposition.
Conséquence 2(développement dans toutes les variables).
Il est évident que si ![]() , ensuite
, ensuite
Donc si la fonction F(X 1 ,X 2 ,…,X n) n'est pas une fonction identiquement fausse, alors elle peut être exprimée par une formule équivalente, qui est une somme logique de différents produits de la forme , et une telle représentation est unique.
La forme de la formule (2) peut être grandement simplifiée. On sait que toute formule de l'algèbre de la logique peut être réduite au moyen de transformations équivalentes à une formule ne contenant que conjonction et négation ou disjonction et négation. En effectuant des transformations équivalentes, plusieurs formules peuvent être obtenues, cependant, une seule d'entre elles aura les propriétés suivantes :
1. Chaque terme logique contient toutes les variables incluses dans la formule F(X 1 ,X 2 ,…,X n).
2. Aucun terme logique ne contient à la fois une variable et sa négation.
3. Tous les termes logiques de la formule sont différents.
4. Aucun terme logique ne contient deux fois la même variable.
Ces quatre propriétés sont appelées propriétés de la perfection(ou propriétés de C).
Si F(X 1 ,X 2 ,…,X n) est donnée par la table de vérité, alors la formule d'algèbre logique correspondante peut être restituée assez simplement. Pour toutes les valeurs d'argument X 1 ,X 2 ,…,X n, auquel F prend la valeur 1, il faut noter la conjonction des variables élémentaires des propositions en prenant pour terme de la conjonction x je, si x je=1, et si x je=0. La disjonction de toutes les conjonctions enregistrées sera la formule nécessaire. À propos des valeurs F 0 vous n'avez pas à vous inquiéter, car le terme correspondant dans la formule sera égal à 0 et peut être ignoré en raison de l'équivalence FÚ 0 ≡ F.
Par exemple, laissez la fonction F(X, y, z) a la table de vérité suivante :
|
X |
y |
z |
F(X, y, z) |
Décomposition de fonctions booléennes en variables.
Soit G un paramètre égal à 0 ou 1. Introduisons la notation :

Il est facile de vérifier en vérifiant que X G = 1 si et seulement si X= G. Il s'ensuit que la conjonction est égale à 1 (ici G est égal à 0 ou 1) si et seulement si ![]() . Par exemple, la conjonction (dans laquelle G 2 \u003d G 1 \u003d 0, G 3 \u003d G 4 \u003d 1) vaut 1 uniquement si X 1 = X 2 = 0, X 3 = X 4 = 1.
. Par exemple, la conjonction (dans laquelle G 2 \u003d G 1 \u003d 0, G 3 \u003d G 4 \u003d 1) vaut 1 uniquement si X 1 = X 2 = 0, X 3 = X 4 = 1.
Théorème 1Toute fonction booléenne f(x 1 ,x 2 ,…,x n) doit être représentée sous la forme suivante :
où 1 ≤ k ≤ n, dans la disjonction est prise sur tous les ensembles de valeurs variables.
Cette représentation s'appelle le développement de la fonction en termes de variables. Par exemple, pour n = 4, k = 2, le développement (3.1) a la forme :
![]() .
.
Démontrons le développement (3.1). Pour ce faire, prenez un ensemble arbitraire de valeurs variables ![]() . Montrons que les membres gauche et droit de la relation (3.1) prennent la même valeur. En effet, depuis X G = 1 si et seulement si X= G, alors parmi 2 une seule conjonction du second membre de (3.1) se transforme en unité, dans laquelle
. Montrons que les membres gauche et droit de la relation (3.1) prennent la même valeur. En effet, depuis X G = 1 si et seulement si X= G, alors parmi 2 une seule conjonction du second membre de (3.1) se transforme en unité, dans laquelle ![]() . Toutes les autres conjonctions sont égales à zéro.
. Toutes les autres conjonctions sont égales à zéro.
Pour cette raison . Comme corollaire du développement (3.1), on obtient les deux développements particuliers suivants.
Expansion variable X n :
Si la fonction booléenne n'est pas une constante 0, alors l'expansion est valide
Expansion dans toutes les variables :
, ![]() (3.3)
(3.3)
où la disjonction est prise sur tous les ensembles ![]() , pour laquelle la valeur de la fonction
, pour laquelle la valeur de la fonction ![]() est égal à 1.
est égal à 1.
La décomposition (3.3) est généralement appelée forme normale disjonctive parfaite (notation abrégée SDNF) de la fonction.
La décomposition (3.3) permet de construire un SDNF. Pour ce faire, dans la table de vérité, marquez toutes les lignes ![]() , dans lequel
, dans lequel ![]() . Pour chacune de ces lignes, nous formons une conjonction, puis connectons toutes les conjonctions résultantes avec un signe de disjonction.
. Pour chacune de ces lignes, nous formons une conjonction, puis connectons toutes les conjonctions résultantes avec un signe de disjonction.
Bien sûr, il existe une correspondance biunivoque entre la table de vérité d'une fonction ![]() et son SDNF. Et cela signifie que le SDNF pour la fonction booléenne est unique.
et son SDNF. Et cela signifie que le SDNF pour la fonction booléenne est unique.
Une seule fonction booléenne qui n'a pas de sdnf est la constante 0.
Exemple 1 Trouver la forme disjonctive parfaite pour une fonction ![]() .
.
Faisons une table de vérité pour cette fonction :
| |
|||||
De là, nous obtenons: ![]() = = .
= = .
Un rôle important dans l'algèbre de la logique est joué par la décomposition suivante des fonctions booléennes.
Théorème 2Toute fonction booléenne ![]() doit être présenté sous la forme suivante :
doit être présenté sous la forme suivante :
où 1≤k≤n, et la conjonction est prise sur les 2 k ensembles de valeurs variables.
En effet, laissez ![]() est un ensemble arbitraire de valeurs variables. Montrons que les parties gauche et droite de la relation (3.4) prennent la même valeur. Depuis seulement quand , alors parmi 2 k disjonctions
est un ensemble arbitraire de valeurs variables. Montrons que les parties gauche et droite de la relation (3.4) prennent la même valeur. Depuis seulement quand , alors parmi 2 k disjonctions ![]() du membre droit de (3.4) un seul est nul, dans lequel
du membre droit de (3.4) un seul est nul, dans lequel ![]() . Toutes les autres disjonctions sont égales à 1.
. Toutes les autres disjonctions sont égales à 1.
Pour cette raison ![]() = =
= = ![]() .
.
Les développements des fonctions booléennes découlent directement du développement (3.4) :
La dernière décomposition est appelée la forme normale conjonctive parfaite (CKNF). La décomposition (3.6) donne un moyen de construire le SKNF. Pour ce faire, dans la table de vérité, nous marquons toutes les lignes dans lesquelles. Pour chacune de ces lignes, nous formons une disjonction ![]() puis nous connectons toutes les conjonctions résultantes avec un signe de conjonction. Bien sûr, il existe une correspondance biunivoque entre la table de vérité d'une fonction
puis nous connectons toutes les conjonctions résultantes avec un signe de conjonction. Bien sûr, il existe une correspondance biunivoque entre la table de vérité d'une fonction ![]() et son SKNF. Et cela signifie que le SKNF pour la fonction booléenne est unique.
et son SKNF. Et cela signifie que le SKNF pour la fonction booléenne est unique.
La seule fonction booléenne qui n'a pas SKNF est la constante 1.
Exemple 2 Trouver la forme normale conjonctive parfaite pour une fonction ![]() .
.
Faisons une table de vérité pour cette fonction.
| |
|||||
De là, nous obtenons SKNF
Formule de forme (notation courte), où ![]() - conjonctions
- conjonctions ![]() appelé forme normale disjonctive (DNF).
appelé forme normale disjonctive (DNF).
En vertu de la définition ci-dessus de DNF, on aura par exemple les expressions : , .
Comme indiqué au paragraphe 2.2, toutes les opérations logiques peuvent être réduites à trois : les conjonctions, les disjonctions et les démentis. De plus, compte tenu de la loi de Morgan, le signe de négation peut être supposé ne s'appliquer qu'aux variables.
Maintenant, en utilisant la loi distributive, nous ouvrons les parenthèses et obtenons la forme normale disjonctive. Donc, le théorème suivant est vrai.
Théorème 3 Pour toute formule de l'algèbre de la logique, il existe une forme normale disjonctive qui lui est équivalente.
La preuve de ce théorème donne un moyen de construire une forme normale disjonctive pour toute formule de l'algèbre de la logique.
Exemple 3 Trouver la forme normale disjonctive de la formule suivante : ![]() .
.
Hors enseigne par la loi ![]() et en appliquant les lois de de Morgan et de la double négation, on obtient :
et en appliquant les lois de de Morgan et de la double négation, on obtient :
![]()
Ensuite, en appliquant la loi de distributivité, nous élargissons les parenthèses
La dernière expression est la forme normale disjonctive.
Voir le formulaire ![]() (notation courte), où sont les disjonctions
(notation courte), où sont les disjonctions ![]() appelé forme normale conjonctive (CNF).
appelé forme normale conjonctive (CNF).
Ce sont, par exemple, des expressions :
![]() , .
, .
Comme indiqué ci-dessus, pour toute formule de l'algèbre de la logique, il existe une forme disjonctive qui lui est équivalente. En utilisant la loi distributive, il est facile d'obtenir un CNF à partir d'un DNF donné.
Donc, le théorème suivant est vrai.
Théorème 4 Pour toute formule de l'algèbre de la logique, il existe une forme normale conjonctive qui lui est équivalente.
La preuve de ce théorème donne un moyen de construire une forme normale conjonctive pour toute formule de l'algèbre de la logique.
Exemple 4 Trouver les formes normales disjonctives et conjonctives de la formule suivante : .
Utiliser la loi ![]() , on exclut le signe . Nous obtenons la formule.
, on exclut le signe . Nous obtenons la formule.
En utilisant la loi de Morgan, on obtient la formule ![]() . En élargissant les parenthèses, on obtient la forme normale disjonctive
. En élargissant les parenthèses, on obtient la forme normale disjonctive
![]() .
.
Pour obtenir la forme normale conjonctive, appliquez la formule ![]() loi distributive, on obtient :
loi distributive, on obtient :
La dernière expression est la forme normale conjonctive. Depuis et , le CNF résultant est équivalent au CNF suivant :
Parmi toutes les formules normales de cette formule, on distingue la forme normale parfaite, à la fois disjonctive et conjonctive. En considérant la décomposition (3), il est facile de voir que la forme normale disjonctive parfaite d'une formule de l'algèbre de la logique contenant exactement n variables distinctes est sa forme normale disjonctive, dans laquelle :
1) toutes les conjonctions sont distinctes par paires ;
2) chaque conjonction contient exactement n variables ;
3) dans chaque conjonction il y a toutes les n variables.
Dans l'exemple 1, nous avons considéré une des manières de construire une SDNF basée sur la compilation d'une table de vérité. La manière suivante de construire SDNF est basée sur l'application des lois de l'algèbre de la logique.
Exemple 5 Trouver la forme disjonctive parfaite de la formule .
En utilisant ça ![]() , on a . Compte tenu des lois de de Morgan et de la double négation, nous avons obtenu une forme normale disjonctive. Ce DNF est équivalent à la formule .
, on a . Compte tenu des lois de de Morgan et de la double négation, nous avons obtenu une forme normale disjonctive. Ce DNF est équivalent à la formule .
En élargissant les parenthèses, on obtient : .
En utilisant la loi d'idempotence, nous obtenons le SDNF requis :
Compte tenu de la décomposition (3.6), il est facile de voir que la forme normale conjonctive parfaite de la formule de l'algèbre de la logique contenant exactement n différentes variables, il y a sa forme normale conjonctive, dans laquelle :
1) toutes les disjonctions sont deux à deux distinctes ;
2) chaque disjonction contient exactement n membres ; identiquement vrai, si elle prend la valeur vrai.
Des exemples de formules identiques vraies sont les formules :
identiquement faux, s'il, avec toutes les valeurs des variables qu'il contient, prend la valeur Mensonge.
Des exemples de formules identiques fausses sont les formules :
La formule de l'algèbre de la logique est généralement appelée faisable, si pour certaines valeurs des variables qui y sont incluses, il prend la valeur vrai.
Des exemples de formules réalisables sont les formules suivantes :
En algèbre de la logique, on peut se poser le problème suivant : indiquer une méthode (algorithme) qui permette pour chaque formule de l'algèbre de la logique de savoir si elle est identiquement vraie ou non. La tâche s'appelle problèmes de résolution.
Considérez les deux façons suivantes pour résoudre ce problème.
Méthode 1 (tableau) Pour déterminer si une formule donnée est identiquement vraie ou non, il suffit de compiler sa table de vérité.
En même temps, cette méthode, bien qu'elle apporte une solution fondamentale au problème de solvabilité, est assez lourde.
Méthode 2 basé sur la réduction des formules à la forme normale.
Théorème 4Une formule de l'algèbre de la logique est identiquement vraie si et seulement si chaque disjonction dans sa forme normale conjonctive contient une variable avec sa négation.
En effet, si chaque disjonction sous forme normale conjonctive contient une variable avec sa négation, alors toutes les disjonctions sont égales à 1, car , . Il s'ensuit que CNF est identiquement vrai.
Soit maintenant la formule donnée identiquement vraie, et soit ![]() il y a une certaine disjonction dans le CNF de cette formule. Supposons que la disjonction donnée ne contienne pas de variable avec sa négation. Dans ce cas, on peut donner la valeur 0 à chaque variable qui n'est pas sous le signe de la négation, et la valeur 1 à chaque variable qui est sous le signe de la négation. Après cette substitution, toutes les disjonctions deviendront égales à 0, donc, le la formule n'est pas identiquement vraie. Nous avons une contradiction.
il y a une certaine disjonction dans le CNF de cette formule. Supposons que la disjonction donnée ne contienne pas de variable avec sa négation. Dans ce cas, on peut donner la valeur 0 à chaque variable qui n'est pas sous le signe de la négation, et la valeur 1 à chaque variable qui est sous le signe de la négation. Après cette substitution, toutes les disjonctions deviendront égales à 0, donc, le la formule n'est pas identiquement vraie. Nous avons une contradiction.
Exemple 7 Découvrez si la formule est identiquement vraie
![]() .
.
En utilisant ça ![]() , on a .
, on a .
En appliquant la loi de distributivité, on obtient CNF :
Puisque chaque disjonction contient une variable avec sa négation, la formule est identiquement vraie.
Comme pour le théorème précédent, le théorème suivant est démontré :
Théorème 5Une formule de l'algèbre de la logique est identiquement fausse si et seulement si chaque conjonction sous sa forme disjonctive contient une variable avec sa négation.
Décomposition de fonctions booléennes en variables. - concepts et types. Classification et caractéristiques de la catégorie "Décomposition des fonctions booléennes en variables." 2017, 2018.