(Attention à la rubrique complémentaire du 04/06/2017 en fin d'article.)

Comptabilité et contrôle ! Les plus de 40 ans devraient bien se souvenir de ce slogan de l’époque de la construction du socialisme et du communisme dans notre pays.

Mais sans une comptabilité bien établie, le fonctionnement efficace ni du pays, ni de la région, ni de l'entreprise, ni du ménage dans n'importe quelle formation socio-économique de la société est impossible ! Pour l'élaboration de prévisions et de plans d'activité et de développement, des données initiales sont nécessaires. Où les emmener ? Seulement un fiable la source est ton données comptables statistiques des périodes précédentes.

Prendre en compte les résultats de leurs activités, collecter et enregistrer des informations, traiter et analyser les données, appliquer les résultats de l'analyse pour prendre les bonnes décisions à l'avenir, à mon avis, toute personne sensée devrait le faire. Ce n'est rien d'autre que l'accumulation et l'utilisation rationnelle de son expérience de vie. Si vous ne conservez pas de trace des données importantes, après un certain temps, vous les oublierez et, en recommençant à résoudre ces problèmes, vous ferez à nouveau les mêmes erreurs que lorsque vous l'avez fait pour la première fois.

"Je me souviens qu'il y a 5 ans, nous fabriquions jusqu'à 1 000 pièces de ces produits par mois, et maintenant nous pouvons à peine en collecter 700 !" On ouvre les statistiques et on voit qu'il y a 5 ans, même 500 pièces n'étaient pas fabriquées...

« Combien coûte un kilomètre de votre voiture, en tenant compte tous frais?" Nous ouvrons les statistiques - 6 roubles / km. Un voyage au travail - 107 roubles. Moins cher qu'un taxi (180 roubles) plus d'une fois et demie. Et il y avait des moments où un taxi était moins cher...

"Combien de temps faut-il pour fabriquer des structures métalliques pour une tour de communication d'angle de 50 m de haut ?" Nous ouvrons les statistiques - et en 5 minutes la réponse est prête...

« Combien coûte la rénovation d’une pièce dans un appartement ? » Nous relevons d'anciens records, effectuons un ajustement en fonction de l'inflation des dernières années, tenons compte du fait que la dernière fois, nous avons acheté des matériaux 10 % moins cher que le prix du marché et - nous connaissons déjà le coût estimé...

En gardant une trace de vos activités professionnelles, vous serez toujours prêt à répondre à la question du patron : « Quand !!!??? ». La tenue d'un dossier familial facilite la planification des achats importants, des vacances et d'autres dépenses futures en prenant les mesures appropriées pour gagner de l'argent supplémentaire ou réduire les dépenses non essentielles aujourd'hui.

Dans cet article, j'utiliserai un exemple simple pour montrer comment les données statistiques collectées peuvent être traitées dans Excel pour une utilisation ultérieure dans la prévision des périodes futures.

Rapprochement dans Excel de données statistiques par une fonction analytique.

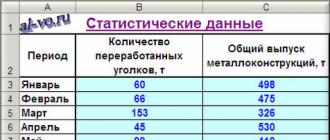
Le site de production fabrique des structures métalliques de construction à partir de produits en tôle et en profilés métalliques. Le chantier fonctionne de manière stable, les commandes sont du même type, le nombre d'ouvriers fluctue légèrement. Il existe des données sur la production de produits au cours des 12 mois précédents et sur la quantité de métal laminé traité pendant ces périodes par groupes : tôles, poutres en I, canaux, angles, tuyaux ronds, sections rectangulaires, produits laminés ronds. Après une analyse préliminaire des données initiales, on a émis l'hypothèse que la production mensuelle totale de structures métalliques dépend de manière significative du nombre d'angles dans les commandes. Vérifions cette hypothèse.

Tout d’abord, quelques mots sur l’approximation. Nous rechercherons une loi - une fonction analytique, c'est-à-dire une fonction donnée par une équation qui décrit mieux que d'autres la dépendance de la production totale de structures métalliques sur le nombre de cornières dans les commandes terminées. Il s'agit de l'approximation, et l'équation trouvée est appelée la fonction d'approximation de la fonction d'origine, donnée sous forme de tableau.

1. Nous activons Excel et plaçons un tableau avec des données statistiques sur la feuille.

2. Ensuite, nous construisons et formatons un nuage de points dans lequel nous définissons les valeurs des arguments sur l'axe X - le nombre de coins traités en tonnes. Sur l'axe Y, nous traçons les valeurs de la fonction d'origine - la production totale de structures métalliques par mois, donnée par le tableau.

3. "Passez" la souris sur l'un des points du graphique et cliquez avec le bouton droit pour appeler le menu contextuel (comme le dit un de mes bons amis, lorsque vous travaillez dans un programme inconnu, lorsque vous ne savez pas quoi faire, n'est-ce pas ?) -cliquez plus souvent...). Dans le menu déroulant, sélectionnez "Ajouter une ligne de tendance...".

4. Dans la fenêtre "Ligne de tendance" qui apparaît, sous l'onglet "Type", sélectionnez "Linéaire".

6. Une ligne droite est apparue sur le graphique, se rapprochant de notre dépendance tabulaire.

En plus de la droite elle-même, nous voyons l'équation de cette droite et, surtout, nous voyons la valeur du paramètre R 2 - la valeur de la fiabilité de l'approximation ! Plus sa valeur est proche de 1, plus la fonction sélectionnée se rapproche avec précision des données tabulaires !

7. Nous construisons des lignes de tendance en utilisant des approximations de puissance, logarithmiques, exponentielles et polynomiales de la même manière que nous avons construit une ligne de tendance linéaire.

Le polynôme du deuxième degré de toutes les fonctions sélectionnées se rapproche le mieux de nos données, il a le coefficient de fiabilité maximum R 2 .

Cependant, je tiens à vous prévenir ! Si vous prenez des polynômes de degrés plus élevés, vous obtiendrez probablement de meilleurs résultats, mais les courbes sembleront complexes…. Ici, il est important de comprendre que nous recherchons une fonction qui a une signification physique. Qu'est-ce que cela signifie? Cela signifie que nous avons besoin d'une fonction d'approximation qui produira des résultats adéquats non seulement dans la plage considérée des valeurs X, mais aussi au-delà, c'est-à-dire qu'elle répondra à la question : « Quel sera le rendement des structures métalliques si le nombre de les angles traités par mois sont inférieurs à 45 et supérieurs à 168 tonnes ! Par conséquent, je ne recommande pas de se laisser emporter par les polynômes de haut degré, et de choisir soigneusement une parabole (polynôme du deuxième degré) !

Nous devons donc choisir une fonction qui non seulement interpole les données tabulaires bien dans la plage de valeurs X = 45 ... 168, mais permet également une extrapolation adéquate en dehors de cette plage. Je choisis dans ce cas une fonction logarithmique, bien que vous puissiez en choisir une linéaire, comme la plus simple. Dans l'exemple considéré, lors du choix d'une approximation linéaire dans Excel, les erreurs seront plus importantes que lors du choix d'une approximation logarithmique, mais pas de beaucoup.

8. Nous supprimons toutes les lignes de tendance du champ du graphique, à l'exception de la fonction logarithmique. Pour ce faire, faites un clic droit sur les lignes inutiles et sélectionnez "Effacer" dans le menu contextuel déroulant.

9. Enfin, nous ajoutons des barres d'erreur aux points de données tabulaires. Pour ce faire, faites un clic droit sur l'un des points du graphique et sélectionnez "Format des séries de données..." dans le menu contextuel et configurez les données dans l'onglet "Y-erreurs" comme indiqué dans la figure ci-dessous.

10. Ensuite, nous faisons un clic droit sur l'une des lignes de plages d'erreur, sélectionnons "Format des barres d'erreur..." dans le menu contextuel et dans la fenêtre "Format des barres d'erreur" sur l'onglet "Affichage", ajustons la couleur et l'épaisseur des lignes.

Tous les autres objets graphiques sont formatés de la même manière.exceller!

Le résultat final du graphique est présenté dans la capture d'écran suivante.

Résultats.

Le résultat de toutes les actions précédentes était la formule résultante pour la fonction d'approximation y=-172,01*ln (x)+1188,2. Connaissant cela, ainsi que le nombre de coins dans l'ensemble mensuel des travaux, il est possible avec un degré de probabilité élevé (± 4% - voir barres d'erreur) de prédire la production totale de structures métalliques pour le mois ! Par exemple, s'il y a 140 tonnes d'angles dans le plan mensuel, la production totale, toutes choses égales par ailleurs, sera très probablement de 338 ± 14 tonnes.

Pour augmenter la fiabilité de l'approximation, il convient de disposer de nombreuses données statistiques. Douze paires de valeurs ne suffisent pas.

D'après la pratique, je dirai que trouver une fonction d'approximation avec un coefficient de fiabilité R 2 >0,87 devrait être considéré comme un bon résultat. Excellent résultat - à R 2 >0,94.

En pratique, il peut être difficile de distinguer un facteur déterminant le plus important (dans notre exemple, la masse de coins recyclés en un mois), mais si vous essayez, vous pourrez toujours le retrouver dans chaque tâche spécifique ! Bien entendu, la production totale mensuelle dépend en réalité de centaines de facteurs, qui nécessitent la prise en compte d’importants coûts de main-d’œuvre des fixateurs de tarifs et d’autres spécialistes. Seul le résultat sera encore approximatif ! Cela vaut-il donc la peine d’en supporter le coût alors qu’il existe une modélisation mathématique bien moins chère !

Dans cet article, je n’ai abordé que la pointe de l’iceberg que sont la collecte, le traitement et l’utilisation pratique des données statistiques. Que j'ai réussi ou non, j'éveille votre intérêt pour ce sujet, j'espère apprendre des commentaires et de l'évaluation de l'article dans les moteurs de recherche.

La question abordée de l'approximation de la fonction d'une variable a une large application pratique dans différentes sphères de la vie. Mais la solution du problème de l'approximation de la fonction a une application bien plus grande plusieurs indépendants variables…. Apprenez-en davantage à ce sujet et bien plus encore dans les articles de blog suivants.

S'abonner aux annonces d'articles dans la fenêtre située à la fin de chaque article ou dans la fenêtre en haut de page.

N'oubliez pas confirmer abonnement en cliquant sur le lien dans une lettre qui vous parviendra au courrier indiqué (peut arriver dans un dossier « Courrier indésirable » )!!!

Je lirai vos commentaires avec intérêt, chers lecteurs ! Écrire!

P.S. (06/04/2017)

Beau remplacement très précis des données tabulaires par une équation simple.

Vous n'êtes pas satisfait de la précision de l'approximation obtenue (R 2<0,95) или вид и набор функций, предлагаемые MS Excel?

Les dimensions de l'expression et la forme de la ligne du polynôme de haut degré approximatif ne sont-elles pas agréables à l'œil ?

Reportez-vous à la page " " pour un résultat plus précis et plus compact de l'ajustement de vos données tabulaires et pour apprendre une technique simple pour résoudre des problèmes d'approximation de haute précision par une fonction d'une variable.

Lors de l'utilisation de l'algorithme d'actions proposé, une fonction très compacte a été trouvée qui fournit la précision d'approximation la plus élevée : R 2 =0,9963 !!!

Approximation de la fonction non linéaire

x 0 /12 /6 /4 /3 5/12 /2

y 0,5 0,483 0,433 0,354 0,25 0,129 0

Puisque l'intervalle de division de la fonction est égal, nous calculons les coefficients de pente suivants des sections correspondantes de la fonction à approximer :

1. Éléments de base pour former des segments de la fonction d'approximation

Formation de la fonction temps

Intervalle de changement :

Temps de redémarrage cyclique : T = 1s

Modélisons maintenant la fonction :

Approximation

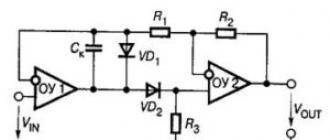
Figure 3.1 - Schéma de résolution de l'équation

Figure 3.2 - Schéma fonctionnel de la formation d'une fonction non linéaire

Ainsi, le côté gauche de l’équation est automatiquement formé. Dans ce cas, on considère classiquement que la dérivée la plus élevée x// est connue, puisque les membres du côté droit de l'équation sont connus et peuvent être connectés aux entrées Y1 (Figure 3.1). L'amplificateur opérationnel U3 agit comme un inverseur de signal +x. Pour simuler x//, il est nécessaire d'introduire un amplificateur subsumateur supplémentaire dans le circuit, aux entrées duquel il est nécessaire d'appliquer des signaux qui simulent le côté droit de l'équation (3.2).

Les échelles de toutes les variables sont calculées en tenant compte du fait que la valeur maximale de la variable machine derrière la valeur absolue est de 10 V :

Mx = 10 / xmax ; Mx/ = 10 / x/max; Mx// = 10 / x //max;

Mon = 10 / ymax. (3.3)

L'échelle de temps est Mt = T / tmax = 1, puisque la simulation du problème est réalisée en temps réel.

Les coefficients de transmission sont calculés pour chaque entrée des amplificateurs intégrateurs.

Pour l'amplificateur U1, les coefficients de transfert sont derrière les formules :

K11 = Mx/b/(MonMt); K12 = Mx/ a2 / (MxMt);

K13 = Mx/ a1 / (MxMt). (3.4)

Pour l'amplificateur U2 :

K21 = Mx/ / (Mx/Mt), (3.5)

et pour l'amplificateur U3 :

K31 = 1. (3,6)

Les contraintes des conditions initiales sont calculées à l'aide des formules :

ux/ (0) = Mx/x/ (0) (-1); ux(0)= Mxx(0) (+1). (3.7)

Le côté droit de l’équation (3.2) est représenté par une fonction non linéaire, donnée par approximation linéaire. Dans ce cas, il faut vérifier que l'erreur d'approximation ne dépasse pas la valeur spécifiée. Le schéma fonctionnel de la formation d'une fonction non linéaire est présenté à la figure 3.2.

Description du schéma de circuit

L'unité de génération de fonction temporelle (F) est réalisée sous la forme d'un (pour former t) ou de deux amplificateurs intégrateurs connectés en série (pour former t2) avec des conditions initiales nulles.

Dans ce cas, lorsque le signal U est appliqué à l'entrée du premier intégrateur, on obtient à sa sortie :

u1(t)= - K11 = - K11Et. (3.8)

En définissant K11E=1, nous avons u1(t)= t.

En sortie du deuxième intégrateur on obtient :

u2(t)= K21 = K11K21Et2 / 2 (3.9)

En mettant K11K21E/2 = 1, nous avons u2(t)= t2.

Des blocs pour former des segments de la fonction d'approximation sont réalisés sous la forme de blocs de diodes de fonctions non linéaires (DBNF), dont la valeur d'entrée est fonction du temps t ou t2. La procédure de calcul et de construction du DBNF est donnée dans.

L'additionneur (SAD) de segments de la fonction d'approximation est implémenté comme un amplificateur final différentiel.

Les conditions initiales pour les intégrateurs du circuit de modélisation sont introduites à l'aide d'un nœud à structure variable (Figure 3.3). Ce schéma peut fonctionner selon deux modes :

a) intégration - avec la position de la clé K en position 1. Dans ce cas, le signal initial du circuit est décrit avec suffisamment de précision par l'équation d'un intégrateur idéal :

u1(t)= - (1 / RC) . (3.10)

Ce mode est utilisé lors de la modélisation d'une tâche. Pour vérifier l'exactitude du choix des paramètres R et C de l'intégrateur, vérifier la valeur de la tension initiale de l'intégrateur en fonction du temps et le temps d'intégration utile dans la limite de l'erreur admissible ?

La valeur de la tension initiale de l'intégrateur

U(t)= - KYE (1 - e - T / [(Ky+1)RC) (3.11)

pendant le temps de simulation T lors de l'intégration du signal d'entrée E à l'aide d'un ampli-op avec gain Ky sans boucle de rétroaction, ne doit pas dépasser la valeur de la variable machine (10 V).

Temps d'intégration

Ti = 2RC (Ku + 1) ?Uadd (3.12)

pour les paramètres de circuit sélectionnés ne doit pas être inférieur au temps de simulation T.

b) le réglage des conditions initiales est mis en œuvre lorsque la clé K est placée sur la position 2. Ce mode est utilisé lors de la préparation du circuit de modélisation pour le processus de solution. Dans ce cas, le signal initial du circuit est décrit par l'équation :

u0(t)= - (R2 /R1) E (3.13)

où u0(t) est la valeur des conditions initiales.

Afin de réduire le temps de formation des conditions initiales et d'assurer un fonctionnement fiable, les paramètres du circuit doivent satisfaire à la condition : R1C1 = R2C.

Construisez un schéma de calcul complet. Dans ce cas, les conventions données au paragraphe 3.1 doivent être utilisées.

En utilisant la capacité des données d'entrée et sources, construisez les diagrammes schématiques des blocs B1 et B2 et connectez-les au bloc PC.

Parmi les différentes méthodes de prévision, il est impossible de ne pas distinguer l'approximation. Avec son aide, vous pouvez effectuer des calculs approximatifs et calculer des indicateurs prévus en remplaçant les objets d'origine par des objets plus simples. Dans Excel, il existe également la possibilité d'utiliser cette méthode pour la prévision et l'analyse. Voyons comment cette méthode peut être appliquée dans le programme spécifié avec les outils intégrés.

Le nom de cette méthode vient du mot latin proxima - « le plus proche ». C'est l'approximation en simplifiant et en lissant les indicateurs connus, en les alignant dans une tendance qui en est la base. Mais cette méthode peut être utilisée non seulement pour la prévision, mais aussi pour l'étude des résultats existants. Après tout, l’approximation est en fait une simplification des données initiales, et la version simplifiée est plus facile à étudier.

Le principal outil avec lequel le lissage est effectué dans Excel est la construction d'une ligne de tendance. L'essentiel est que, sur la base des indicateurs existants, le graphique de la fonction pour les périodes futures est en train d'être complété. Comme vous pouvez le deviner, l’objectif principal de la ligne de tendance est de faire des prévisions ou d’identifier une tendance générale.

Mais il peut être construit en utilisant l’un des cinq types d’approximation suivants :

• Linéaire;
• exponentiel;
• logarithmique;
• polynôme;
• Pouvoir.

Examinons chacune des options plus en détail séparément.

Méthode 1 : lissage linéaire

Tout d'abord, considérons la version la plus simple de l'approximation, à savoir l'utilisation d'une fonction linéaire. Nous y reviendrons plus en détail, car nous exposerons les points généraux caractéristiques d'autres méthodes, à savoir le tracé et quelques autres nuances, sur lesquelles nous ne nous attarderons pas lors de l'examen des options ultérieures.

Tout d’abord, construisons un graphique sur la base duquel nous effectuerons la procédure de lissage. Pour construire un graphique, prenons un tableau dans lequel sont indiqués sur une base mensuelle le coût d'une unité de production produite par l'entreprise et le bénéfice correspondant sur une période donnée. La fonction graphique que nous allons construire affichera la dépendance de l'augmentation du profit sur la diminution du coût de production.

Le lissage utilisé dans ce cas est décrit par la formule suivante :

Dans notre cas particulier, la formule prend la forme suivante :

y=-0,1156x+72,255

La valeur de la fiabilité de l'approximation est égale à 0,9418 , ce qui est un résultat assez acceptable qualifiant le lissage de fiable.

Méthode 2 : approximation exponentielle

Examinons maintenant le type d'approximation exponentielle dans Excel.

La forme générale de la fonction de lissage est la suivante :

Où e est la base du logarithme népérien.

Dans notre cas particulier, la formule prenait la forme suivante :

y=6282,7*e^(-0,012*x)

Méthode 3 : lissage logarithmique

C'est maintenant au tour d'envisager la méthode d'approximation logarithmique.

En général, la formule de lissage ressemble à ceci :

Où dans est le logarithme népérien. D'où le nom de la méthode.

Dans notre cas, la formule prend la forme suivante :

y=-62,81ln(x)+404,96

Méthode 4 : Lissage polynomial

Le moment est venu d’envisager la méthode du lissage polynomial.

La formule qui décrit ce type de lissage a pris la forme suivante :

y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09

Méthode 5 : lissage de puissance

En conclusion, considérons la méthode d'approximation de puissance dans Excel.

Cette méthode est utilisée efficacement en cas de modification intensive des données fonctionnelles. Il est important de noter que cette option n'est applicable que si la fonction et l'argument ne prennent pas de valeurs négatives ou nulles.

La formule générale décrivant cette méthode est la suivante :

Dans notre cas particulier, cela ressemble à ceci :

y = 6E+18x^(-6,512)

Comme vous pouvez le constater, en utilisant les données spécifiques que nous avons utilisées pour l'exemple, la méthode d'approximation polynomiale avec un polynôme du sixième degré a montré le plus haut niveau de fiabilité ( 0,9844 ), le niveau de fiabilité le plus bas pour la méthode linéaire ( 0,9418 ). Mais cela ne signifie pas du tout que la même tendance se produira si l’on utilise d’autres exemples. Non, le niveau d'efficacité des méthodes ci-dessus peut varier considérablement en fonction du type spécifique de fonction pour lequel la ligne de tendance sera construite. Ainsi, si la méthode choisie est la plus efficace pour cette fonction, cela ne veut pas du tout dire qu’elle sera également optimale dans une autre situation.

Si vous ne pouvez pas déterminer immédiatement, sur la base des recommandations ci-dessus, quel type d'approximation convient spécifiquement à votre cas, il est alors logique d'essayer toutes les méthodes. Après avoir tracé la ligne de tendance et visualisé son niveau de confiance, vous pouvez choisir la meilleure option.

Méthodes numériques pour résoudre des problèmes

Radiophysique et électronique

(Didacticiel)

Voronej 2009

Le manuel a été préparé au Département d'électronique du département physique

Faculté de l'Université d'État de Voronej.

Des méthodes pour résoudre les problèmes liés à l'analyse automatisée des circuits électroniques sont envisagées. Les concepts de base de la théorie des graphes sont exposés. Une formulation matricielle-topologique des lois de Kirchhoff est donnée. Les méthodes matricielles-topologiques les plus connues sont décrites : méthode du potentiel nodal, méthode du courant de boucle, méthode des modèles discrets, méthode hybride, méthode des variables d'état.

1. Approximation de caractéristiques non linéaires. Interpolation. 6

1.1. Polynômes de Newton et de Lagrange 6

1.2. Interpolation spline 8

1.3. Moindres carrés 9

2. Systèmes d'équations algébriques 28

2.1. Systèmes d'équations linéaires. Méthode Gauss. 28

2.2. Systèmes d'équations clairsemés. Factorisation LU. 36

2.3. Résolution d'équations non linéaires 37

2.4. Résolution de systèmes d'équations non linéaires 40

2.5. Équations différentielles. 44

2. Méthodes de recherche d'un extremum. Optimisation. 28

2.1. Méthodes de recherche extrêmes. 36

2.2. Recherche passive 28

2.3. Recherche séquentielle 36

2.4. Optimisation multidimensionnelle 37

Références 47

Approximation de caractéristiques non linéaires. Interpolation.

1.1. Polynômes de Newton et de Lagrange.

Lors de la résolution de nombreux problèmes, il devient nécessaire de remplacer la fonction f, sur laquelle il existe des informations incomplètes ou dont la forme est trop complexe, par une fonction F plus simple et plus pratique, proche dans un sens ou dans un autre de f, donnant son approximation représentation. Pour l'approximation (approximation), on utilise des fonctions F appartenant à une certaine classe, par exemple des polynômes algébriques d'un degré donné. Il existe de nombreuses variantes différentes du problème d'approximation de fonctions, selon les fonctions f qui sont approximées, les fonctions F utilisées pour l'approximation, la manière dont la proximité de f et F est comprise, et ainsi de suite.

L'une des méthodes de construction de fonctions approximatives est l'interpolation, lorsqu'il est nécessaire qu'en certains points (nœuds d'interpolation) les valeurs de la fonction d'origine f et de la fonction d'approximation F coïncident. Dans un cas plus général, les valeurs de les dérivés à des moments donnés devraient coïncider.

L'interpolation de fonction est utilisée pour remplacer une fonction difficile à calculer par une autre plus facile à calculer ; pour une récupération approximative d'une fonction à partir de ses valeurs en des points individuels ; pour la différenciation numérique et l'intégration de fonctions ; pour la solution numérique d'équations non linéaires et différentielles, etc.

Le problème d'interpolation le plus simple est le suivant. Pour certaines fonctions sur un segment, n + 1 valeurs sont données aux points , appelés nœuds d'interpolation. Dans lequel . Il est nécessaire de construire une fonction d'interpolation F(x) qui prend les mêmes valeurs aux nœuds d'interpolation que f(x) :

F(x 0) \u003d f (x 0), F (x 1) \u003d f (x 1), ..., F (x n) \u003d f (x n)

Géométriquement, cela signifie trouver une courbe d'un certain type passant par un système de points donné (x i , y i), i = 0,1,…,n.

Si les valeurs de l'argument dépassent la région, alors on parle d'extrapolation - la continuation de la fonction au-delà de la région de sa définition.

Le plus souvent, la fonction F(x) est construite comme un polynôme algébrique. Il existe plusieurs représentations de polynômes d'interpolation algébrique.

L'une des méthodes d'interpolation de fonctions qui prennent des valeurs en points est la construction d'un polynôme de Lagrange, qui a la forme suivante :

Le degré du polynôme d'interpolation passant par n+1 nœuds d'interpolation est n.

Il résulte de la forme du polynôme de Lagrange que l'ajout d'un nouveau point nodal entraîne une modification de tous les membres du polynôme. C'est l'inconvénient de la formule de Lagrange. Mais la méthode Lagrange contient le nombre minimum d'opérations arithmétiques.

Pour construire des polynômes de Lagrange de degrés croissants, le schéma itératif suivant (schéma d'Aitken) peut être appliqué.

Les polynômes passant par deux points (x i , y i) , (x j , y j) (i=0,1,…,n-1 ; j=i+1,…,n) peuvent être représentés comme suit :

Polynômes passant par trois points (x i , y i) , (x j , y j) , (x k , y k)

(i=0,…,n-2 ; j=i+1,…,n-1 ; k=j+1,…,n) peut être exprimé en termes de polynômes L ij et L jk :

Les polynômes pour quatre points (x i , y i) , (x j , y j) , (x k , y k) , (x l , y l) sont construits à partir des polynômes L ijk et L jkl :

Le processus se poursuit jusqu'à l'obtention d'un polynôme passant par n points donnés.

L'algorithme de calcul de la valeur du polynôme de Lagrange au point XX, qui met en œuvre le schéma d'Aitken, peut s'écrire à l'aide de l'opérateur :

pour (int je = 0; je

pour (int je = 0; je<=N-2;i++)Здесь не нужно слово int, программа

cela sera perçu comme une erreur - re-déclaration d'une variable,

la variable i a déjà été déclarée

pour (int j=i+1;j<=N-1;j++)

F[j]=((arg-x[i])*F[j]-(arg-x[j])*F[i])/(x[j]-x[i]);

où le tableau F représente les valeurs intermédiaires du polynôme de Lagrange. Initialement, F[I] doit être égal à y i . Après exécution des boucles, F[N] est la valeur du polynôme de Lagrange de degré N au point XX.

Les formules de Newton sont une autre forme de représentation du polynôme d'interpolation. Soit des nœuds d'interpolation équidistants ; je=0,1,…,n ; - étape d'interpolation.

La première formule d'interpolation de Newton, utilisée pour l'interpolation directe, est :

C’est ce qu’on appelle les différences (finies) du ième ordre. Ils sont définis ainsi :

Argument normalisé.

En , la formule d'interpolation de Newton se transforme en série de Taylor.

La 2ème formule d'interpolation de Newton est utilisée pour interpoler "à l'envers" :

Dans la dernière entrée, au lieu de différences (appelées différences « en avant »), des différences « en arrière » sont utilisées :

Dans le cas de nœuds inégalement espacés, ce qu'on appelle. différences divisées

Dans ce cas, le polynôme d'interpolation sous la forme de Newton a la forme

Contrairement à la formule de Lagrange, ajout d'une nouvelle paire de valeurs. (x n +1 , y n +1) se réduit ici à ajouter un nouveau terme. Par conséquent, le nombre de nœuds d’interpolation peut être facilement augmenté sans répéter l’intégralité du calcul. Cela vous permet d'évaluer la précision de l'interpolation. Cependant, les formules de Newton nécessitent plus d'arithmétique que les formules de Lagrange.

Pour n=1, on obtient la formule d'interpolation linéaire :

Pour n=2 nous aurons la formule d'interpolation parabolique :

Lors de l'interpolation de fonctions, les polynômes algébriques de haut degré sont rarement utilisés en raison des coûts de calcul importants et des erreurs importantes dans le calcul des valeurs.

En pratique, l'interpolation linéaire par morceaux ou parabolique par morceaux est le plus souvent utilisée.

Avec interpolation linéaire par morceaux, la fonction f(x) sur l'intervalle (i=0,1,…,n-1) est approchée par un segment de droite

L'algorithme de calcul qui implémente l'interpolation linéaire par morceaux peut être écrit à l'aide de l'opérateur :

pour (int je = 0; je

si ((arg>=Fx[i]) && (arg<=Fx))

res=Fy[i]+(Fy-Fy[i])*(arg-Fx[i])/(Fx-Fx[i]);

A l'aide de la première boucle, on recherche où se situe le point souhaité.

En interpolation parabolique par morceaux, le polynôme est construit en utilisant les 3 points nodaux les plus proches de la valeur d'argument donnée.

L'algorithme de calcul qui implémente l'interpolation parabolique par morceaux peut être écrit à l'aide de l'opérateur :

pour (int je = 0; je

y0=Fy ; Pour i=0, l'élément n'existe pas !

x0 = Effet ; Le même

res=y0+(y1-y0)*(arg-x0)/(x1-x0)+(1/(x2-x0))*(arg-x0)*(arg-x1)*(((y2-y1) /(x2-x1))-((y1-y0)/(x1-x0)));

Le recours à l'interpolation n'est pas toujours conseillé. Lors du traitement de données expérimentales, il est souhaitable de lisser la fonction. L'approximation des dépendances expérimentales par la méthode des moindres carrés procède de l'exigence de minimiser l'erreur quadratique moyenne

Les coefficients du polynôme d'approximation sont trouvés à partir de la solution d'un système de m + 1 équations linéaires, ce qu'on appelle. équations "normales", k=0,1,…,m

En plus des polynômes algébriques, les polynômes trigonométriques sont largement utilisés pour approximer des fonctions.

(voir "analyse harmonique numérique").

Les splines sont un appareil efficace pour approximer une fonction. La spline nécessite la coïncidence de ses valeurs et dérivées aux points nodaux avec la fonction interpolée f(x) et ses dérivées jusqu'à un certain ordre. Cependant, la construction de splines nécessite dans certains cas des coûts de calcul importants.

Les caractéristiques des éléments non linéaires réels, qui sont généralement déterminées à l'aide d'études expérimentales, ont une forme complexe et sont présentées sous forme de tableaux ou de graphiques. Parallèlement, pour l'analyse et le calcul des circuits, une représentation analytique des caractéristiques est nécessaire, c'est-à-dire représentation sous forme de fonctions assez simples. Le processus de compilation d'une expression analytique pour les caractéristiques présentées graphiquement ou sous forme de tableau est appelé approximation.

L'approximation résout les problèmes suivants :

1. Détermination de la zone d'approximation, qui dépend de la plage des signaux d'entrée.

2. Détermination de la précision de l'approximation. Il est clair que l'approximation donne une représentation approximative de la caractéristique sous la forme d'une expression analytique. Par conséquent, il est nécessaire de quantifier le degré d’approximation de la fonction d’approximation par rapport à la caractéristique déterminée expérimentalement. Le plus couramment utilisé:

indicateur d'approximation uniforme - la fonction d'approximation ne doit pas différer de la fonction donnée de plus d'un certain nombre , c'est-à-dire

;

indicateur d'approximation du carré moyen - la fonction d'approximation ne doit pas différer de la fonction donnée dans l'approximation du carré moyen de plus d'un certain nombre, c'est-à-dire

;

approximation nodale (interpolation) - la fonction d'approximation doit coïncider avec la fonction donnée en certains points sélectionnés.

Il existe différentes méthodes d'approximation. Le plus souvent, pour l'approximation des caractéristiques I – V, on utilise une approximation par un polynôme de puissance et une approximation linéaire par morceaux, moins souvent - une approximation utilisant des fonctions exponentielles, trigonométriques ou spéciales (Bessel, Hermite, etc.).

7.2.1. Approximation par un polynôme de puissance

La caractéristique courant-tension non linéaire au voisinage du point de fonctionnement est représentée par un nombre fini de termes dans la série de Taylor :

Le nombre de termes dans la série est déterminé par la précision de l'approximation requise. Plus il y a de termes dans la série, plus l’approximation est précise. En pratique, la précision requise est obtenue par approximation par des polynômes du deuxième et du troisième degrés. Chances - ce sont des nombres qui sont tout simplement déterminés à partir du graphique VAC illustré par un exemple.

Exemple.

Pour se rapprocher de celui montré sur la Fig. 7.1,un CVC au voisinage du point de fonctionnement par un polynôme puissance du deuxième degré, soit polynôme de la forme

Choisissons la zone d'approximation de 0,2 V à 0,6 V. Pour résoudre le problème, il faut déterminer trois coefficients . On se limite donc à trois points nodaux (au milieu et aux limites de la plage sélectionnée), pour lesquels on compose un système de trois équations :

Riz. 7.1. Approximation des caractéristiques IV d'un transistor

En résolvant le système d'équations, nous déterminons , , . Par conséquent, l’expression analytique décrivant la courbe I – V a la forme

A noter que l'approximation par un polynôme de puissance est principalement utilisée pour décrire des fragments individuels de caractéristiques. En cas d'écarts importants du signal d'entrée par rapport au point de fonctionnement, la précision de l'approximation peut se détériorer considérablement.

Si le CVC n'est pas spécifié graphiquement, mais par une fonction analytique et qu'il devient nécessaire de le représenter comme un polynôme de puissance, alors les coefficients sont calculés à l'aide de la formule bien connue

.

Il est facile de voir que est la pente I – V au point de fonctionnement. La valeur de la pente dépend essentiellement de la position du point de fonctionnement.

Dans certains cas, il est plus pratique de représenter la caractéristique par la série de Maclaurin

7.2.2. approximation linéaire par morceaux

Si l'amplitude du signal d'entrée varie sur une large plage, la caractéristique I-V peut alors être approchée par une ligne brisée composée de plusieurs segments de ligne droite. Sur la fig. 7.1b montre la caractéristique courant-tension du transistor, approximée par trois segments de ligne.

Formule mathématique du CVC approximatif

Ce type d'approximation est associé à deux paramètres importants d'un élément non linéaire : la tension du début de la caractéristique et sa pente. Pour augmenter la précision de l'approximation, augmentez le nombre de segments de ligne. Cependant, cela complique la formule mathématique du CVC.